うっちーこんにちは！うっちーです
年金アドバイザー3級試験は、基本知識編（問1～30）については一般的な５肢択一問題なのですが、技能･応用編（問31~50）は出題がちょっと特殊です。
５肢択一式ではあるのですが、事例が提示されて、それに対するアドバイスや年金の計算式などを選んでいくという問題になっています。
うっちー一見とっつきにくそうなのですが、コツを覚えて解けるようになるとなかなかおもしろいのです。
そのコツをお伝えしたくて、技能･応用編の論点整理と過去問解説を掲載しています。
まずは、技能･応用編でめちゃめちゃ大事になるテクニックと知識をご紹介します。
和暦の換算方法
年アド試験では、登場人物の生年月日などは和暦で記載されています。
FP試験では西暦で出題されるので、それに慣れているとちょっと勝手がちがってくるかもしれません。
事例にでてくる人物はほぼ昭和生まれなのですが、それから平成をまたいで、現在は令和。
そこで試験では、
令和 ⇔ 平成 ⇔ 昭和
の換算をしょっちゅうやることになります。
例えば、平成は30年までですので、令和4年は 4＋30＝34で平成34年相当と変換できます。
次の数字をプラスすると和暦の年を過去の和暦相当の年に変換することができます。
『令和』⇒『平成』は ＋30
『平成』⇒『昭和』は ＋63
『令和』⇒『昭和』は ＋93
例）
・平成30年は昭和何年？
H30＋63＝昭和93年
・令和6年は昭和何年？
R6＋93＝昭和99年
これとは逆に、昭和相当の年から93を引くと令和に変換できます。
例）
昭和34年生まれの人が65歳になるのは令和何年？
S34＋65＝S99
S99－93＝令和6年
月数の計算方法
年アドでは次のような、期間の月数を数えられないと解けない問題がでてきます。
「昭和51年4月から昭和54年2月までが何ヵ月間あるか？」
早く正確に数えられると、技能･応用編の問題を解くのが劇的に楽になります。
基本はこちらです。
終わり ー 始め ＋ １
「１月から12月までが何ヵ月あるか？」をこれに当てはめると
12月－1月＋１＝12ヵ月
と求めることができます。
では次に、「令和4年1月から令和5年12月までが何ヵ月あるか？」だと、どうでしょう。2年間だから24ヵ月というのはすぐわかるのですが、これを計算で求めるとしたら…
じつは、和暦の年数に12をかけて月数にすれば、さっきと同じ要領で計算できます。
（5年×12＋12月）ー（4年×12＋1月）＋１
＝72－49＋１＝24
期間の終わりと始めの差を求めたいだけなので、令和4年の1月が実際に令和の最初の月から数えて何ヵ月目かということは無視して、機械的に計算してください。
練習問題
うっちーではここで問題です
昭和59年4月から令和6年3月までの期間は何ヵ月あるでしょうか？
手順 ⇒ 令和4年を昭和に換算した上で、年数に12倍して月数を足します。そして「終わりー始め＋１」です。
答えはこのページの一番下に書いておきますね。
期間の計算，なぜそうなるの？
先ほどご紹介した期間の計算がなぜ「終わり ー 始め ＋１」という式になるのかについて解説します。
意味なんてわかってなくても計算式に機械的に当てはめればいいので、この話はぶっちゃけ蛇足です。
うっちー気になる方だけ、次の文をタップしてご覧ください。
期間が「終わり ー 始め ＋１」で計算できる理屈
ここに1月から12月のマスがあります。
質問です！「3月～12月は何ヵ月（何マス）あるでしょうか？」
塗りつぶしのマスを数えていくと10マスあるので、10ヵ月です☟
では、これを計算で求める場合、どういう式になるでしょうか？
全体の12マスから、3月よりも手前の1月,2月の２マスを切り取れば（差し引けば）いいですね☟
計算式は
「全体のマス数 ー 3月より手前のマスの数 」ですから
１２－（３ー１）
そして、計算式の中の（ ）を取り除くと、（ ）の中の－は＋に反転します。
うっちー算数の受業で習った、かすかな記憶…
すると、この式になります。
１２－３＋１
これをイメージで示すとこんな感じです☟
全体の12マスからいったん3月までの３マス分を切り取ってから…
マスをひとつ戻します（＋１します）。
結果は10マス（10ヵ月）になります。
「12‐(3-1) 」でも「12‐3＋1」でも、結果は同じです。
これを言い変えて、
全体のマス ⇒ 終点（の月数）
切り取るマス ⇒ 始点（の月数）
としたものが、
終わり ー 始め ＋ １
の計算式です。
理屈を解説してみましたが、要はこの式に機械的に当てはめていただければOKです。
歳をとる日
期間の計算に関連して、歳をとる日がいつなのかも大事な要素です。
技能･応用編では、「20歳以上～〇年〇月までの期間」や「〇年〇月～60歳未満の期間」などの月数を正確に数えられないと解けない問題がでてきます。
例えば、10月で二十歳を迎える人がいたとして、「20歳以上～次の3月までの期間が何ヵ月あるか？」を問われたとします。
下の図で塗りつぶしのマスを数えると6ヵ月だと答えられますね。
これだけだと簡単に思えるのですが…じつは、年齢にはちょっとしたひっかけが存在するのです。
うっちーそれがこちらです
年齢が上がるのは誕生日の前日
これは、「年齢計算ニ関スル法律」という法律で定められています。
一般的には年齢が上がったことを祝うのは誕生日当日なので、変な感じがしますね。
もし、誕生日当日に年齢が上がる決まりだと、うるう年の2月29日に生まれた人は4年一回しか歳がとれないことになります。
「前日」と決まっているおかげで2月28日に年齢が上がるため、毎年歳をとることができるのです。
年齢が上がるのが誕生日の前日ということは、誕生日が1日の人は前月末日に歳をとることになります。
という事は、年齢が上がる月がひと月前倒しになります。
例）年齢が上がる日は？
・10月2日生まれ⇒10月1日
・10月1日生まれ⇒9月30日
そうすると、先ほどマスで数えた「20歳以上～次の3月までの期間」が変わってきます。
10月2日生まれと10月1日生まれで比べてみましょう。
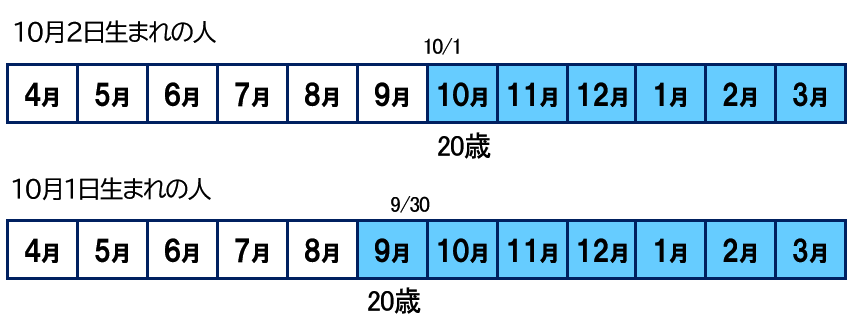
10月2日生まれは先ほどと同じなのですが、10月1日生まれの場合は20歳になる月が9月になります。
9月から3月までは７マスありますので、「20歳に達する月～次の3月までの期間」は7ヵ月になります。さっきよりもひと月増えましたね。
うっちーこのちがい、要注意ですよ！！
事例には1日生まれの人がよくいるんです。
ひっかけの論点を作りやすいので、年アド試験には1日生まれの人が不自然なほどよく登場します。
（本来、1日生まれの人は確率的に12/365≒3.3%ほどしかいないはずなんですけどね。）
過去の傾向ではＡさんやHさんの問題に多いのですが、他の問題にいることもあります。
年齢が上がる時刻は？？
「年齢が上がるのは誕生日の前日」ということはわかったけど、「じゃあ、年齢が上がる時刻は何時なのか？」という疑問が残りますね。
例えば、10月1日生まれの人は9月30日の何時に年齢が上がるのでしょうか？
細かすぎて試験には関係ありませんが、説明しておきます。
うっちー気になる方は、次の文をタップしてご覧ください。
年齢が上がる時刻について
じつは、時刻についても先ほどの『年齢計算ニ関スル法律』を基にした見解があります。
その時刻とは『午後12時』です。
午後12時と午前0時は同じ時刻。真夜中に時計の針が真上に重なった時です。
ただし、午後12時と午前0時では日付けがちがいます。下の時計の図で言うと午後12時は9/30ですが、午前0時は日付けが変わった10/1の時刻になります。
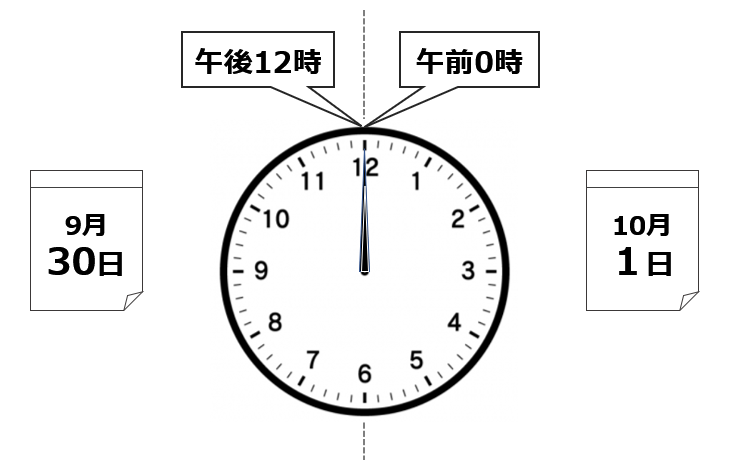
誕生日の前日に年齢が上がるというのは、前日の午後12時に年齢が上がるという解釈になっています。
誕生日が10月1日の人は、その前日の9月30日の午後12時に年齢が上がるのです。
こまか～いようですけど、このわずかな違いが先ほどの期間の計算のようにひと月分の期間の違いを生むこともあるので、詳細に決めておかないといけないのです。
友達に、年齢が上がった瞬間におめでとうLINEを送ってあげようとするなら、お誕生日の前日の午後12時（＝当日の午前0時）がそのタイミングということになりますね。
ここまでわかってなくても問題は解けます。トリビア的なものと思ってください。
練習問題の答え
期間の計算式のところで出した練習問題の解答です。
求める期間は
S59.4～R6.3
R6を昭和に換算します。
R6.3＋99＝S99.3
年に12をかけて月数をプラスします。
59×12＋4＝712
99×12＋3＝1191
終わりー始め＋1
1191ー712＋１
＝480
答えは480ヵ月でした。
昭和59年4月に20歳を迎えた人は、その月から数えて令和6年3月でちょうど40年（480ヵ月）経過の60歳になるということですね。
期間の計算は技能･応用編の問題でよく使うので、問題を解きながら繰り返して慣れておきましょう！
うっちーくれぐれも＋１を忘れずに！
今回参考にした法律のリンクです。公的機関のものではいまいちわかりづらかったので、Wikiの記事を掲載いたします。
過去問だけでは網羅できない論点の押さえにおすすめ！
私が愛読している年金の本はこちら！
＼ 過去問をわかりやすく説明 ／
＼ 年アドコンテンツの一覧はこちら ／
